
Figure A1)
Theory, text, illustrations, and editing by Ken Sasaki
4-bar path analysis by Peter Ejvinsson
Spanish Version translated by Antonio Osuna
Additional translation and edition for the web y José Rubio
“Linkage” suspension simulation by Gergely Kovacs
© Kenneth M. Sasaki 2001, all rights reserved
{The authors welcome the reposting or reprinting of this page or any part of it, so long as full credit is given to the authors}
Warning: the proof at this page seems not to be correct, see Comment on 'Suspension Path Analysis'.
Many with whom this author has regular contact have a particular interest in the following situation involving a bike not undergoing acceleration. In addition, as is pointed out in the “Ellsworth’s ‘Instant Center Tracking’ (ICT)” section, this example has particular relevance in showing problems with ICT theory. For these reasons, in addition to PCL being so widely accepted, we will explore it a little further.
We proceed with a proof by counterexample to show that PCL is incorrect even for a bike undergoing no acceleration. We construct the counterexample as follows:
Recall that all of the forces on a coasting bike sum to zero. Bicycle acceleration acts on the frame members through the rear axle. So we eliminate the torques generated due to bike acceleration under pedaling by clamping the bike at the rear axle, in a friction wheel equipped trainer. We can dispense with the fork term by turning the bike sideways and imagining some alternative force to gravity keeping the rider attached to the seat. Figure A1) diagrams this:

Figure A1)
Next, for ease of visualization and calculation, we replace the frame members with a couple of poles at 90° to each other. With the “main triangle” pole taken as having a reasonable, non-uniform mass distribution, this situation is not far from reality in many cases. As per our calculations in “An Intuitive Look at Forces and Torques.”, we have left out the crank and will neglect the rotating parts of the rider’s body (feet and lower legs). Figure A2) shows this situation:
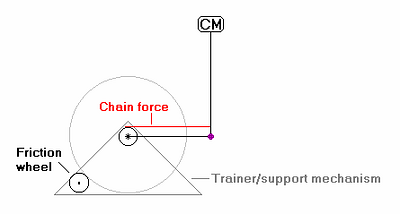
Figure A2)
Looking at this picture, it should already be obvious that the pivot is not the right place for the chain, if we want the poles to stay at (or at least near) 90 deg. As the chain is tensioned, the two poles must rotate around the rear axle en unison to achieve no shock activation. If the chain is at the pivot, no torque will be on the main triangle pole to rotate it back.
But let’s go ahead and calculate:
We neglect the centripetal acceleration created as the bodies start to rotate around the rear axle, since this is minuscule.
This leaves only the chain torque and the body interaction torques.
Since the poles are at 90°, the swingarm pole will not create an interaction torque on the main triangle pole. However, recalling that for every action there is an equal and opposite reaction, we see that the main triangle will create an interaction torque on the swing arm. Recalling the quantities from Figure 2.12) in “An Intuitive Look at Forces and Torques.”, we express the torque equation for the swingarm as:
![]() ,
,
where tSI is the interaction torque from the main triangle, m is the mass of the main triangle, and “a” is the main triangle linear acceleration.
Now a = a*SL, so we have:
![]() .
.
But we should recognize m*SL2 as a moment of inertia. That is, if we calculate an effective IS' as the inherent moment of inertia of the swingarm plus a moment induced by the mass of the main triangle, then we have:
![]() .
.
Or, with IS' = (IS + m*SL2),
![]() .
.
Now we have an equation involving only the chain torque. One often finds that equations can be set up in a number of ways depending on how things are defined – in this case leading to a very interesting result. This also exemplifies the assertion made in regard to Equation 8) in “An Intuitive Look at Forces and Torques.” that the torques will eliminate T in all expressions except that for the fork.
Following the previously done calculations for h in constructing Equation 8), we have:
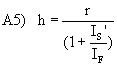 .
.
We are left with only the first term from Equation 8) – that for the chain torque, as expected.
We can see that Equation A5) matches our intuition exactly. It tells us that the heavier the main triangle and rider are compared to the swing arm, the farther away we move from PCL. Even with only the chain force under consideration, the very common PCL theory could be true only if the mass of the rider/main triangle is zero! This again is in perfect accord with our intuitive study of Figure A2) above. The rider/main triangle is very large compared to the swing arm –about 40 times as large. Assuming a reasonable mass distribution for the rider/main triangle, one will find that h equals about 80% of r.
After these calculations, it should be easy for anyone to verify that PCL is not correct, even for a rider pedaling a bike while floating in free space [again remember our pole and wheel experiment from Figure 2.5), with the earth as a very large front triangle]. In this case, an almost parallel chain line is appropriate.
The fundamental problem with PCL for non-accelerating bikes is the neglect of the wheel (the same neglect found in Ellsworth’s ICT). If the chain were attached directly between the main triangle and swingarm, then the pivot would be the place to pull, neglecting acceleration. But then we would not have a bike. Because bicycles have wheels, PCL is incorrect.