Figure 2.9)
Warning: the proof at this page seems not to be correct, see Comment on 'Suspension Path Analysis'.
Read this section if:
You want a semi-qualitative analysis of forces and torques going on within a suspension bicycle. Understanding everything in this section is not important to understanding Path Analysis. This is just for people who want to go a little deeper.
Read just the conclusions in this section (written bold) if:
You want just the conclusions of the analysis for application to other sections. The conclusions should not be too difficult to understand, so we suggest that one at least give them a quick read. Whatever one does not understand probably will not matter too much, but one might pick up some useful information for the trouble.
Skip this section if:
You are just interested in using Path Analysis to make conclusions and comparisons regarding various bikes.
This section is among the two most difficult in the work.
We here do an intuitive study of forces and torques in a mono-pivot non-URT to understand the things of which a suspension theory must account. This will help us further understand what goes on in a suspension and the limitations on what any viable design can really accomplish. We try to keep the math to a minimum, however we will be making some minimal calculations to demonstrate certain solutions in principle. Those with a less technical background can ignore the calculations and look directly at the conclusions, which are written bold.
The most important lesson of this section is that mass distribution is an important consideration in the physics of full suspension bicycles. No quantitative theory can be correct without this consideration.
It is common practice to take no reaction of the rear shock to pedaling as the goal, so we will follow.
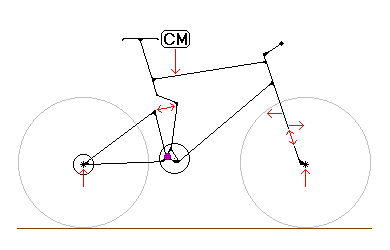
Figure 2.9) shows the front and rear triangles of a “coasting” mono-pivot, with the various forces acting on them, minus friction in the hubs and air, which we neglect (the forces are not drawn to scale). “CM” indicates the rough position for the rider/main triangle center of mass.

Figure 2.9)
All forces sum to zero when there is no pedaling. For this reason, we need examine only those forces and torques that appear as the result of a pedal stroke. Figure 2.10) shows the picture without the coasting forces drawn.
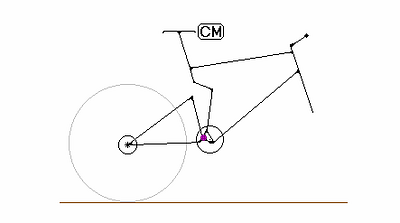
Figure 2.10)
There are a number of ways one might go about analyzing this situation. We will use the torque equation:
1) I*a = å t.
Here, I is the moment of inertia of the body in question, a is the angular acceleration, and å t is the sum of the torques on the body. This is the angular analogue to ma = å F. Using equation 1), we will examine what issues are involved in keeping the torque balance between the main triangle and swingarm, about the main pivot, as close to zero as possible.
For precise calculation, this method is not very useful, since some of the torques are not easy to state explicitly and all of the torques are time-dependant (all except chain torque depending on the positions and movements of the two frame members, which will change with time through the pedal stroke). We can thus glimpse the complexity of any completely rigorous analysis. But for us and our mainly intuitive study, this method will be very useful, since we can use it to explore a number of interesting points with minimal math.
We start with a comment on chain force.
One must be very careful when thinking about lines of force in that magnitude, direction, and location are all important. Even equivalent gear ratios generally produce lines of force that differ in magnitude and direction as well as location.
Figure 2.11) shows a drive train with two possibilities for a 1-1 gearing. L is the crank lever, R1 and R2 are the respective cog radii, and T1 and T2 are the chain tensions for each case.
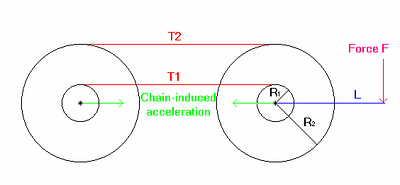
Figure 2.11)
If a force F is induced at L with resulting tension in the chain (examining one case at a time), the resulting torque equation for the crank is (assuming a non-URT just for ease of calculation):
2) I*a = F*L - T1*r = F*L - T2*R
Thus, T1/R = T2/r. That is, the chain tension decreases as the front cog radius increases – a rather interesting result. So, even the two 1-1 situations will generally not produce equivalent results for suspension activation under pedaling. This actually should not surprise us, since the energy transmitted through the system should be the same in both cases. Energy can be expressed as T*d, where T is the chain tension and d is the length of the chain that passes by some fixed point like the seat tube. Since a greater chain length is pulled in a bigger chain ring for a given rotation of the crank, we need a lesser force to keep the energy constant.
Continuing: Figure 2.12) shows the diagram for the calculations to follow. The partially pictured triangle represents the main triangle, to which the crank is attached. The lower horizontal line represents the swing arm of length SL. R is the front cog radius and r is the rear cog radius. L is the length of the crank arm. F is the force of a pedal stroke. T is the resulting chain tension. h is the perpendicular distance from the chain to the pivot, D is the perpendicular distance from the pivot to the force line at the BB induced by the chain tension, and d is the perpendicular distance from the pivot to the line through the rear axle that is parallel to the chain tension. q is the angle of the chain from the swingarm axis.
Recall the Center of Mass/force phenomenon described in Figure 2.6) of the “Center of Mass” section; it applies both to the proactive force F acting on the crank and to the reactive force T from the chain, both with results at the center.
We have not pictured all of the forces present on the suspension members, but only those induced as a result of a pedal stroke that are relevant for our calculations.
We assume that the crank axle and main pivot are close together relative to frame size. (A few frames such as the The Rocky Mountain ETS-X70 and the i-Drive differ from this significantly, but this will not impact on the relevant points, and all conclusions will be valid for all suspension frames). This allows us to approximate the force at the pivot from the crank axle as if the two were coaxial. We also assume that the crank mass is negligible. This will allow us to equate forces on the chain ring and crank arm to resulting forces at the crank axle.
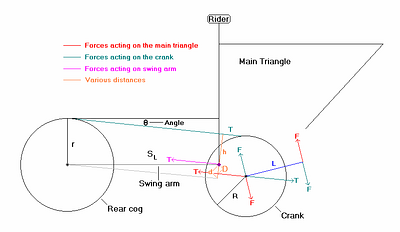
Click to enlarge
Figure 2.12)
In the following calculations, the reference frame for the main triangle torque equation is centered at the suspension main pivot and does not rotate (with respect to the earth). The reference frame for the swing arm torque equation is centered at the rear axle and also does not rotate. Since both reference frames do not rotate, the bodies will stay at a static angle to each other if their angular accelerations are the same (the initial angular velocities are both zero). IF and IS are, respectively, the main triangle moment of inertia about the main pivot and the swing arm moment of inertia about the rear axle. tFi and tSi denote the various torques on the respective bodies about their coordinate origins, which include the torques due to the chain, fork/front wheel (friction and inertia), bicycle acceleration (the most commonly recognized of which is squat), the crank rotation and lower rotating parts of the rider's body, and also the torques due to the interactions of the two frame members [we do some further work with these interaction torques in Appendix A) “PCL Problems; Some Further Calculations.”, should anyone have questions as to exactly what these are].
{An aside: One should not be too concerned about the following detail, but the astute reader will note that we are using two different non-inertial reference frames for each bicycle frame member. The bicycle acceleration and interaction torques are the fictitious torques in these reference frames.}
The torque equations for the rider/main triangle and swing arm are then, respectively:
![]()
and
![]() .
.
Achieving the stated goal of minimizing suspension reaction to pedaling generally involves finding the best place for the main pivot relative to the chain force line for an assumed condition (mass distribution, etc.). To do this, one must express the chain torque in terms of h and solve for this quantity in the proper equation. Fortunately the chain and pedal torques are easy to state in equation and will allow us to get a formula in principle for the desired relation of pivot and chain.
Let tFC denote the torque on the main triangle due to pedaling and the resulting chain tension.
Noting that with a negligible crank mass, F = T*R/L, the torque on the main triangle due to the pedal stroke and resulting chain tension is:
5) tFC = F*L – T*D = T*R - T*D = T*(R-D) = T*h.
So we see that, neglecting the mass of the crank, the torque on the main triangle from pedaling is just as if we had been pulling on the chain from a point on the main triangle that is a perpendicular distance h above the pivot – a very interesting result (see Ola Helenius for an interesting intuitive argument for this result, though we are not exactly sure where it is on his site). However, one must be very careful not to take this result too far; as we have seen, for a given pedal force, the larger the radius of the front cog, the lower will be the chain tension.
Let tSC denote the torque on the swingarm from the chain (again, ultimately from pedal force). Again, since in practice the pivot is relatively close to the BB compared to the frame size, we approximate the force on the swing arm at the pivot as that of the chain force induced at the BB (these values will be very close for typical frames). With this approximation, we have:
![]()
To have the torque balance between the main triangle and swingarm about the main pivot equal to zero (to get no reaction of the rear shock), we want the front and rear triangles to rotate en unison – that is, we want the aF = aS. Solving for the a's in equations 3) and 4) and setting the two expressions equal to each other we get:
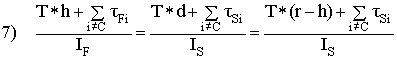 .
.
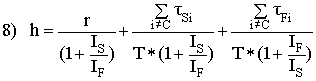 .
.
This is the zero torque balance formula for the main pivot position, relative to the chain line for a non-URT mono-pivot (with pivot not too far from the BB compared to the size of the frame – again, almost always the case).
One might conclude that h depends on T, as T appears in the denominator of the last two terms. We state without proof that T will appear as a factor in all of the torques, just as it did for the chain torque, with the exception of that resulting from the fork. So with the noted fork exception, h does not depend on T. [In “PCL Problems; Some Further Calculations.”, we give an example of how the torques, for the most part, eliminate T from equation 8).]
We may draw the following conclusions from equation 8):
First, notice that the moments of inertia for both bodies are in all terms. This tells us that it will be impossible to construct any sort of a quantitative suspension theory without taking into account mass and its distribution. Mass distribution will be of equal consideration for all other suspension types. This rules out certain “Special Point” Theories, such as the most naive “Pivot at the Chain Line” (PCL) theories.
The second thing we notice is that since the torque values are time-dependant, h will also be time-dependant through the pedal stroke. We thus see that there is no single “proper pivot point” (or points), exactly, through an entire pedal stroke. In addition, we note as a matter of intuition, that as the rider makes a pedal stroke, the system of frame members, on average, will rotate back relative to the rear axle (a ¹ 0). Between pedal strokes, the frame members will fall back down, and not in such a way as to keep the rear shock inactive without help from friction in the pivots. This further tells us that it is impossible for any rear suspension geometry to be completely non-reactive to pedaling, without static friction.
The time-dependant nature of our mono-pivot situation is also common to all other suspension types, since frame member orientation changes through the pedal stroke in all of these bikes as well. In particular, mono-pivots can approximate a zero torque balance about the main pivot as well as any 4-bar, through the pedal stroke.
The effects of changing frame member orientation are relatively small, but we note them as a warning against all theories that purport to completely eliminate shock activation to pedaling, in principle, based on geometry (even if there is an assumption for mass distribution), such as “Special Point” Theories.
Since the frame orientation effects are relatively small, a single geometry can behave relatively uniformly through the pedal stroke. Suspension geometry can thus keep pedal effects on the shock to a minimum, on average, and let friction do the rest. Pedaling effects on the rear shock can be made small compared to any significant bump, so a good suspension with the right amount of friction can effectively control oscillations, while remaining supple enough to absorb any significant bump.
Lastly, as a matter of intuition, we note that in any suspension, the less the rear shock extends during a pedal stroke, the more the front shock extends. There will be loss to friction either way. The ideal proportion of front and rear shock activation will be that which minimizes sympathetic oscillation.