Figure 3.7)
Read this section.
It is not technically difficult and the “Natural Mirror” conceptual device is the most easily understood confirmation for the validity of Path Analysis.
The best intuitive confirmation that one can have for the validity of Path Analysis is to imagine putting two different suspension mechanisms on one bike simultaneously. There would be no conflict between them as long as the component paths were the same for both mechanisms. Shortly after I first published the “simultaneous suspension”, a particular version of my idea was proposed that would have one side of a bike constructed from a mono-pivot and the other from a 4-bar with a circular rear axle path. More generally, we may construct a bike with two different suspension mechanisms on either side, each having the same component paths. I will refer to such a bike as a “natural mirror” or simply “mirror” suspension bike, since the true nature of each suspension is mirrored on the other side.
We can include the paths of all components as part of a natural mirror analysis, or only those for which we may have a particular interest. For example, if we wish to compare only wheel paths, we may imagine pairing up frames with identical wheel paths and it will not matter whether other components, such as the shock mounts, also have identical paths.
In evaluating the validity of a theory, physicists often examine certain “obvious” cases to see if the theory makes sense. Here we examine several designs with circular rear axle paths, to demonstrate that they will all perform identically under pedaling (suspension rate adjustments accounted for in the last example).
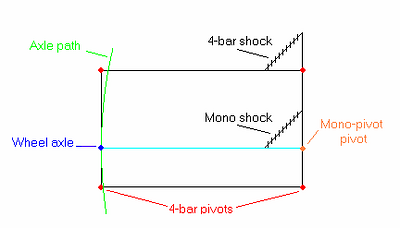
Suppose we start on one side of a mirror bike with a 4-bar suspension in which the “bars” determine a parallelogram – that is, the upper arm is equal in length to the lower arm and the forward arm (the main triangle between the two forward pivots) is equal to the rear. We call this a “parallel” 4-bar. The wheel path (both for pivot on the chain stay or seat stay) is circular.
On the other side of the bike, we can use a mono-pivot, with main pivot at the same height above the 4-bar main pivot as the wheel axle is above the 4-bar rear pivot.
We refer to this bike as a “parallel/mono” mirror and both sides produce the same path.
We could even make the shock mounts have equivalent paths by mounting a shock to the mono-pivot in the same way that we mount a shock to one of the horizontal 4-bar arms. Each side of the bike will perform exactly the same as the other. Figure 3.7) shows both of the above suspensions from the side.

Figure 3.7)
Let us now consider another 4-bar. This time though, we will make the two forward pivots coaxial to produce what we call a “pp-coaxial” 4-bar. The pivots will still be physically attached to the main triangle separately and thus the suspension will constitute a true 4-bar. The wheel in this case also has a circular path and thus this suspension can be put in with either of the other two. We will call this 4-bar combined with a mono-pivot a “pp-coaxial/mono” mirror. See Figure 3.8) for this example.
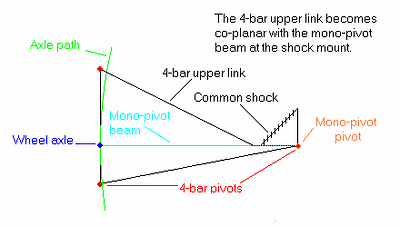
Figure 3.8)
Lastly, let us consider a 4-bar with rear wheel mounted coaxially with the rear lower pivot. It does not matter whether the rear wheel is mounted physically to the chain stay or the seat stay, both will behave the same, as the wheel will have the same path. We will call a mirror bike with this suspension and a mono-pivot a “wp-coaxial/mono” mirror. The configurations of the 4-bar upper links contribute only to the suspension rate in this case. Adjusting the relative paths of the shock mounts as well as the “internal” rates of the shocks may be done to more or less match the over all suspension rates of the two sides. Figure 3.9) shows this mechanism.
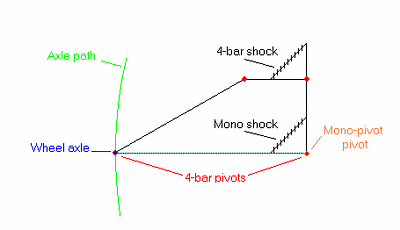
Figure 3.9)
All of these are examples of very different suspension configurations that will behave exactly the same while not under braking (shock tuning accounted in the last case), because the rear axle paths are the same – namely circular. The shock mount paths in the first two examples are not identical in space, but are identical in relative motion and so cause no conflict.