

A well-known problem at recumbents amd mountain bikes with rearwheel-suspension is, that they move upwards and downwards (pogo) through the suspension, because of the varying pedalforce of the rider. This is not only annoying, it also causes loss of energy at the damper of the suspension. Specially with a worn damper and at low gears at the mountains pogo and accompanying losses can be considerable.
This page contains a method to compute an optimal position for the middle chainwheel of a recumbent with rear derailleur or gear hub or a combination of these gear systems. At the optimal position for all gears the pedal induced bob or "pogo" will be eliminated. The method is based on the basic principle of the "optimal anti-squat diagonal", which is also used when tuning racing cars, motorcycles and mountain bikes.
For (mountain)bikes, that do not have a middle chainwheel, the same result can be achieved by optimal positioning of the front chainwheel.
This page is written after reading the article "Never seasick again" of Rembrandt Bakker at the Dutch recumbent-magazine Ligfiets& 2004-3. My recumbent at that moment, a Speedliner BlueGlide, bobbed after replacement of the suspension as never before and I was looking for an explanation. The article gave an explanation and a computation, but also mentioned derogotary calculations
The article of Rembrandt Bakker has been compared to the formulas of Bert Bruynooghe and Kees van Malssen and with the graphical simulation of Walter Zorn (this Java program can be started under Windows 10 and 11 with Microsoft Edge in Internet Explorer mode or can be started under Chrome, Chromium or Edge with the CheerpJ extension).
The three methods gave different results.
On this page the reasoning of Bert Bruynooghe and Kees van Malssen is used. Explanation of the used calculations is given and it is indicated, how losses caused by pedal induced bob can be minimized.
At the American WISIL-site computations are made by Charlie Ollinger using a model in Unigraphics NX CAD. The same positions of chain, swing arm and middle chain wheel, as found at this page, are optimal.

In a graphical model the reader can manipulate the geometry of the recumbent and check the effect on pogo (squat).
The geometry of the recumbent can be changed by moving parts (chain, wheels etc.) by mouse or by specifying sizes (in mm.).
By modifying the field HubGearRatio the gear ratio of a simulated internal gear hub can be changed.
Field "Pogo" displays the degree of bob. With the button "Optimize Pogo", the middle chain wheel will be positioned optimally, with minimal value at the field "Pogo" (0 = no bob). If the "HubGearRatio" is not equal 1.0, then for a minimal pogo also the angle of the swing arm is modified.
If the chain line and the swing arm intersect within the wheelbase, the forces on the frame are shown, which are caused by the pedaling force.
The "black" arrow shows the sum of the chain force and the force via the swing arm.
If the "HubGearRatio" is not equal to 1.0, then the "red" arrow shows the moment force on the rear fork and shows the "magenta" arrow the total sum of the forces.
The "blue" horizontal and vertical arrows under the rear wheel and above the front axle show the forces on the bike caused by pedaling force. If there is no front suspension, the vertical force above the front axle has no effect and only the horizontal force is effective there.
For the fields "AntiSquat", "SwingArmAntiS" and "ChainAntiS", see MTB, Squat, Anti-Squat.
For the fields "PKickBack...", see Relation between pedalkickback and pogo.
Examples are made for my current recumbents the Nazca Pioneer with 26-inch-wheels and the Quest with 20- and 26-inch-wheel, the Nazca Gaucho with 26-inch-wheels, the Nazca Quetzal tandem with 26-inch-wheels and Rohloff-gear-hub, the Challenge Chamsun with 28-inch-wheels and Rohloff-gear-hub, the low racer of Walter Zorn, the Speedliner BlueGlide with 20- and 26-inch-wheel and the Giant Reign Mountainbike.
At the magazin Ligfiets& 2006-5 an article has been published, which explains with a minimal of formulas the principle of the pogo-free rear swing-arm construction.
The same reasoning can also be applied to a pogo-free front swing-arm construction.
We start with a recumbent (or other bike) with suspension at the rear wheel, which is pedal-driven at the front wheel.
The pedalforce of the cyclist causes a friction force Fd between road and front tire,
which pulls the bike forwards (to the right at the figure).
This force passes through the frontaxle to the bike, where it causes some acceleration to the bike.
This force is equal to friction force Fd, but has the opposite direction.
The mass of bike and rider resist with a force which can be situated at the center of gravity which is approximately located at the rider's umbilicus.
The consequence of these forces is that the frame will try to rotate, which compresses the suspension between frame and rear swing arm.
There will be an extra pressure on the rear wheel and an extra reaction force Fw from the road at the wheel.
At the frontwheel pressure on the road will decrease and therefore also pressure from the road on the wheel will decrease, here painted by a downwards pointing force Fw with the same size. It looks like accelleration moves the center of gravity to the rear. The rear of the bike will move downwards. This is called "squat".
The forces Fd at the center of gravity and Fw at the rear wheel result into a torque at the contact point of the front wheel at the road.
To avoid rotation of the bike, the sum of these torques should be zero:
Fd * Hcg + Fw * Lwb = 0, or
Fw = - Fd * Hcg / Lwb ,
where Hcg is height of center of gravity and Lwb is length of wheelbase.
The pedalforce continuously varies, which results into accceleration or slowing down of the center of gravity and results into pressing in and extending the suspension.
The bike will bob with a frequency, that is twice the pedal-frequency and there will be "bob-losses" at the damper of the suspension.
Bob will be enlarged by:
We now examine a rearwheel-driven recumbent with rear suspension.
Also at this situation the pedalforce causes the forces Fd at the center of gravity and Fw at the rearwheel.
Because the bike doesnot rotate, the sum of torques at the contact point of the front wheel at the road again must be zero:
Fd * Hcg + Fw * Lwb = 0.
We now look at the relation between chainforce Fc and driving force Fd.
At the next figure there is a rear wheel with a chain wheel.
Via the chain there is a force Fc on the chain wheel.
The chain force causes a driving force at the road (Fd).
Because the wheel is able to rotate freely, the sum of the torque of the two forces must be zero:
Fc * rcr = Fd * rwr
where rcr is the radius of the rear chainwheel and rwr the radius of the rear wheel.
Because the torque of the forces at the axle is zero, the sum of the forces (Fdc) should direct through the axle (sum of torques of forces = torque of sum of forces).
If we want to compute Fdc , we just can add the vectors of the forces Fc and Fd and position them at the center of the wheel.
In next figure the vectors of chain force Fc, the driving force Fd and the force induced by mass inertia Fw are added graphically.
If the angle of the rear swing arm is equal to the angle of the total force Ftot, there will be no squat or pogo-effect.
We now try to find the ideal chain angle for a given angle of the swing arm.
At this calculation we are not interested in the total force, but in the component (Fvsa), that is perpendicular on the swing arm.
This component causes pogo and must be processed by the suspension.
At the previous figure hsa is the angle between swing arm and the horizontal axis, and hsaC is the angle between swing arm and chain.
We compute Fvsa by adding for each force the component perpendicualar on the swing arm.
This leads to the the formula:
Fvsa = Fc * sin(hsaC) + Fd * sin(hsa) - Fw * cos(hsa)
Fvsa = Fc * sin(hsaC) + Fc * (rcr /rwr) * sin(hsa) - Fc * (Hcg / Lwb) * (rcr/ rwr) * cos(hsa)
Fvsa = Fc * (sin(hsaC) + (rcr /rwr) * sin(hsa) - (Hcg / Lwb) * (rcr/ rwr) * cos(hsa))
We define the pogo-percentage caused by chain force (Fc) as:
pogo_percentage_chainforce = (Fvsa / Fc) * 100.
The torques at the crank (with radius rcl) and at the front chain ring (radius rcf) provide the link between pedal force and chain force:
Fcl * rcl = Fc * rcf
Fcl = Fc * (rcf / rcl)
The aimed pogo-percentage caused by pedal force (Fcl) is defined as:
pogo_percentage = (Fvsa / Fcl) * 100.
pogo_percentage = (Fvsa * (rcl / rcf) / Fc) * 100
pogo_percentage = (sin(hsaC) + (rcr /rwr) * sin(hsa) - (Hcg / Lwb) * (rcr/ rwr) * cos(hsa))* (rcl / rcf) * 100
This definition had the effect, that at a positive value the swing arm is moved downwards and the bicycle frame upwards. (as is previously shown).
If at the graphical simulation the rear cog is enlarged, we see the pogo-percentage changing.
The ideal chain line is dependent of the chosen gear.
On the one hand the powers Fd and Fw increase proportional to the radius of the rear cog.
The angle between chain and swing arm must be larger to compensate this.
On the other hand at a larger rear cog this angle between chain and swing arm automatically increases.
At the previous paragraph we saw, that at a given gear there will be no pogo, if the angle between chain and swing arm is correctly chosen.
This means that the middle chain wheel must touch this optimal chain line at a random position.
If we compute a second chain line for another rear gear and let the middle chain wheel touch both lines at the crossing of both lines, we have for two different gears an optimal position.
This method is applied at the graphic simulation, if one presses the "Optimize" button. If the current rear cog is small we use a 30-teeth rear cog as second gear, if the current rear cog is large, we use a 12-teeth rear cog as second gear, to compute the optimum.
The result of this manipulation is surprising.
Pogo is not only minimal (zero) at the used cog sizes, but also at the other cog sizes.
If we look at the position of the middle chain wheel it also appears that for all kinds of recumbents the middle chain wheel must touch the line of the swing arm.!!
This observation can be deduced as follows. If the middle chain wheel touches the line of the swing arm, the formula sin(hsaC) = rcr / L applies, where L is the distance between rear axle and middle chain wgeel. There is no pogo, if the perpendicular force at the swing arm Fvsa = 0.
If we fill this in the previously derived formula for Fvsa, we get the next formula for the distance L:
L = rwr / ((Hcg / Lwb ) * cos(hsa ) - sin(hsa ))
We can write the former formule as:
Hcg / Lwb = (rwr + L * sin(hsa)) / (L * cos(hsa)).
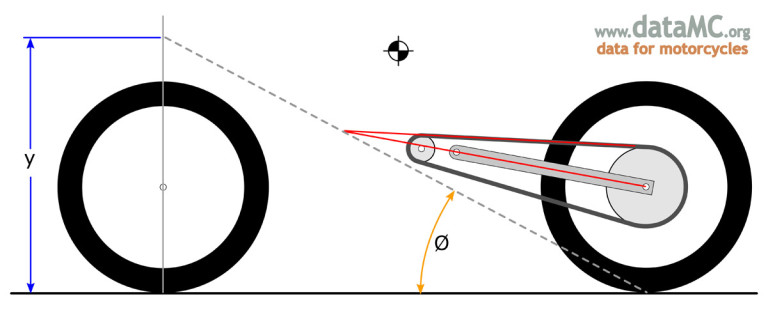
The height y of the optimal point can be computed by:
y = rwr + L *sin(hsa)
The horizontal distance x to the point of contact of rear wheel and road:
x = L * cos(hsa)
If we fill in x and y en y at the first formule, we get the result:
y / x = Hcg / Lwb.
All optimal points are on a line from point of contact of rear wheel and road to a point vertical above the front axle at the same height as the center of gravity.
At the graphical simulation this line (the optimal diagonal) is colored red.
The point of intersection of this line with the line of the swing arm is the optimal point at a given angle of the swing arm!
If in the graphical simulation the chainline and swing arm intersect within the wheelbase, the intersection shows the sum of chain and swing arm forces on the frame, which is caused by the pedaling force (black).
In all cases, also at a sub-optimal setting, the extension of the displayed power arrow (black) runs through the contact point of the rear wheel with the road. The forward, horizontal force is everywhere equal to the forward force Fd at the point of contact of the rear wheel with the road. The vertical force increases with the height of the intersection.
At first glance, it seems impossible to eliminate pogo with a hub gear. The chain angle is constant here and thus can not be used to compensate for the changing downward force, which is the result of a changing forward force when choosing another (hub) gear (see e.g. paragraph "Pogo-sticking of a suspended bicycle" op https://www.sheldonbrown.com/twist-internal.html#design ).
With hub gear, however, there is an extra force present. With a hub gear, the torque on the rear chain wheel is not equal to the torque on the rear wheel. The difference is compensated at the hub gear by a torque on the swing arm (see e.g. https://www.sheldonbrown.com/twist-internal.html#nuts ).
This gives next formulas:
Fd = Fc * (rcr / (hubgear * rwr)))
Fw = Fd * (Hcg / Lwb) = Fc * ((Hcg / Lwb) * (rcr / (hubgear * rwr)))
The torque at the rear wheel, where L is length of swing arm:
Fhubgear * L = Fc * rcr - Fd * rwr
Fhubgear = Fc * rcr * (1- (1 / hubgear)) / L
Also here we are not interested in the total force, but in the component (Fvsa), that is perpendicular on the swing arm. This component causes pogo and must be handle by the suspension:
Fvsa = Fc * (sin(hsaC ) + (rcr / (hubgear * rwr)) * sin(hsa ) - (Hcg / Lwb ) * (rcr / (hubgear * rwr)) * cos(hsa ) - rcr * (1- (1 / hubgear)) / L)
If the middle chain wheel touches the pivot point of the swing arm next formula is valid: sin(hsaC = rcr / L. Pogo is eliminated if Fvsa = 0.
The length of the swing arm:
L = rwr / ((Hcg / Lwb ) * cos(hsa ) - sin(hsa ))
At this formula the variable hubgear is missing. This means, pogo (bob) is absent at any hub gear!
Also the formula is exactly the same as at the derailleur gear. Therefore the optimal location is at the same optimal diagonal as was found at the derailleur!
The effect of this can be examined by changing the field HubGearRatio at the simulation. E.g. at the Nexus 7-speed the ratio can vary from 0.632 to 1.545. The Rohloff 14 speed varies from 0.278 to 1.466.
With the button "Optimize Pogo", the middle chain wheel is optimally positioned. If the "HubGearRatio" is not equal 1.0, then for a minimal pogo also the angle of the swing arm is modified.
Also at a gear hub it is possible to make an optimal configuration, to avoid pogo for every gear, but therefore the extra requirement is needed, that the pivot of the swingarm is positioned at the "optimal diagonal".
IF in the graphical simulation the chainline and swing arm intersect within the wheelbase, the intersection will show the sum of chain and chainstay forces on the frame , which is caused by the pedaling force (black). If a gear hub is present, the moment force on the rear fork (red) and the total sum of the forces (magenta) are also shown .
In all cases, even with a sub-optimal setting, the extension of the arrow shown for the total force (magenta) runs through the contact point of the rear wheel with the road. Also in the presence of a gear hub, the forward force at any height of the intersection is equal to the forward force Fd on the road. The vertical force increases with the height of the intersection.
The forward, horizontal force is in all cases equal to the forward force Fd at the contact point of the rear wheel with the road. The vertical force increases with the height of the intersection.
As long as the front wheel maintains contact with the road, this vertical force is compensated by the pressure on the front wheel.
At the graphical simulation the horizontal "blue" arrow above the front axle is showing the final effective force at the frame caused by the pedaling force.
If this horizontal force is not directed through the center of gravity ("cg"), the frame will rotate. Above the front axle the frame cannot move vertically and so will rotate about a point directly above the front axle, at the same height as the center of gravity.
This is shown below in a simple pogo model of a bicycle with rear suspension.
At the link Suspension a closer look is taken at the losses that occur with a sub-optimal pogo setting, where the ultimate effective force is not directed through the center of gravity.

Also at mountainbikes bob is an important issue. Here they speak about squat and anti-squat. There is 100% anti-squat, if the squat (bob caused by varying pedal forces) completely is compensated by the angle of the swing arm combined with the pulling chain line. 100% anti-squat results into the same optimal position of the intersection between swing arm and chain line as shown above at this web page. Already at 2005 a computation of antisquat for mountainbikes is published (see http://forums.mtbr.com/general-discussion/how-chain-affects-suspension-final-word-120875.html). For a more recent publication see e.g. here.
The percentage anti-squat of a bike at the field "AntiSquatBike" is computed by dividing the ratio of the y- and x-coordinates of the intersection by the ratio of center of gravity and wheel base. At the mountainbike above this is 110%. At the graphical simulation anti-squat is shown at the field "BikeAntiSquat. 100% anti-squat is equivalent to 0% pogo.
The "Pogo" values are not in all cases in accordance with the "BikeAntiSquat" values. If one compares the values of "BikeAntiSquat" at different corners of the rear fork and a fixed value of "Pogo", than there are big differences, especially at low pivoting points, as is the case with a low recumbent bike.
The reason for this is that in the calculation of pogo the force is determined, which must be applied by the spring in order to prevent the compression of the bicycle. This is a force perpendicular to the rear fork. If the angle of the rear fork is large, the spring only needs to apply a small part of the downward force because of this angle.
To illustrate the differences, the field "SuspAntiSquat" is also calculated, which represents the percentage of the Squat, which is compensated by the construction of the bicycle at the Suspension.
In the determination of antisquat, no account is taken of the fact that at low speed ratio the driving force at the rear wheel is much larger and consequently also the bob. Because at the definition of pogo the speed ratio is taken into account, pogo gives a more realistic picture of the expected bob.
Mountainbikes do not have a middle chain wheel. Therefore the chain line varies a lot, if the front chain wheel is switched. This makes 100% anti-squat for all speeds impossible for mountainbikes. See the graphical simulation Giant Reign Mountainbike.
As soon as the cyclist is sitting down, the extra weight will press the suspension.
How far the suspension is pressed depends on properties of the suspension, its position on the bike and the sag-setting.
The result is a changed angle of the swing arm, changed height of the center of gravity and a changed optimal position of the middle chain wheel.
An easy adjustable sag or an adjustible position of the middle chain wheel could be a solution to compensate different weights of cyclist and luggage.
When filling the height of the pivot point and mid-wheel of an existing bicycle in the graphical simulation, values must therefore be used for a bicycle with pressed suspension by the weight of the rider.
It has previously been observed that a non-driven, suspended front wheel will always cause some bob at the bicycle, because the squat force can not be compensated by the chain force. This needs some addendum, if both wheels are suspended.
The graphical simulation shows that the full vertical squat force pushes the front fork upwards when the rear wheel antisquat is 100% and the bob is minimized. Minimizing pogo on the rear wheel is at the expense of an increase in pogo on the suspended front wheel!
This problem does not seem to be solvable by another construction of the bicycle. This can, however, be partially overcome by special suspension.

At these suspension the damping is not constant, but depending on the speed of compression of the suspension. We speak of "high-speed" and "low-speed" damping. The "low-speed" damping mainly dampens the squat phenomena and is therefore chosen as large as possible. Large damping also reduces the power losses due to squat. See here
Pedalkickback is well known from mountainbikes.
If a rear wheel with suspension passes a large unevenness at the road (e.g. a treeroot) and bounces, the suspension suddenly gets shorter. This can give so called pedalkickback on the pulling chain and pedals.
Pedalkickback is well known at the mountainbike world. For a computation see https://polebicycles.com/wp-content/uploads/2015/06/PedalKickbackCalculation.pdf.
Pedalkickback occurs when the rear fork and pulling chain are not positioned horizontally.
Two effects are responsible for this.
First of all because of the shorter suspension, the length of the wheelbase might change. This effect is called "PKickBackLow" at the graphical simulation.
At a high recumbent with the pivot of the swingarm often positioned higher than the rear axle, the rear wheel will be pushed a little bit to the rear, which causes pedalkickback.
At a low recumbent the wheel will be pushed forward, which causes some extra chain length.
Also because of the shorter suspension the length of the chain between rear cog and pulling front chain wheel might change. This effect is called "PKickBackHigh" at the graphical simulation.
If the chain runs parallel to the swingarm this change of length is almost zero.
If the angle between chain and swing arm is negative (the chain runs downwards from rear cog towards the swing arm), then the chain length of the pulling chain initially increases if the suspension shortens, which causes kickback at the pedal.
At a recumbent with optimal chain line to eliminate pogo, pedalkickback will not be an important problem. Besides kickback is somewhat caught by the internal suspension within a long chain.
The graphical simulation computes kickback at the pedal (in millimeters), which is caused by a moving the rear wheel 20 millimeter upwards because of a sudden unevenness at the road.
At a graph one can also see the relation between vertical rearwheel-movement and pedalkickback. A positive "RearWheel Deviation" indicates that the rear wheel is pushed up, a positive "PedalKickBack" means a kickback on the pedal.
At the following paragraphs we assume, that the nike is configured for miniamal pogo..
If the center of gravity is on the road and therefore there is no force Fw at the rear axle, then at an optimal position of the middle chainwheel there is no pogo and pedalkickback is neglectible or even negagtive. If the centerpoint is raised and length of swing arm is fixed, then we see that at the optimized position (no-pogo) pedalkickback slowly increases. Pogo induced by mass inertia can be compensated, but the price is a higher pedalkickback.
A lower gear uses a larger rear chainwheel, increasing the absolute values of "PKickBackHigh" and "PKickBackLow" .
Using a lower hubgear only causes an increasing "PKickBackLow".
At a low recumbent with the pivot of the swingarm often positioned lower than the rear axle, "PKickBackHigh" and "PKickBackLow" are opposite. In that case wit a low hubgear it is possible, that both pogo and pedalkickback are zero. So pedalkickback is not a requirement for zero pogo.
See PedalKickBack_HubGear.
A rearwheel-driven recumbent with rear suspension seems to be designed, to eliminate pogo. For all gears there is a common optimal point of intersection between chain line and swing arm. It is positioned at the imaginary (red) line from point of contact of rear wheel and road to a point vertical above the front axle at the same height as the center of gravity. minimized by chosing an optimal position of the middle chainwheel at the frame. The middle chainwheel should touch this point of intersection.
Also for all hub gears there is the same common optimal point of intersection. An additional requirement is that the pivot point of the rear swing arm coincides with this point of intersection. If the middle chain wheel (or if absent the front chain wheel) correctly touches this point of intersection, the setting is also optimal for every rear derailleur gear!
It is not possible to achieve an optimal position for a number of recumbent bicycles. With low recumbent bicycles, such as a velomobile, the chain must pass under the seat. With a less optimal position, one could choose to eliminate pogo only for the most used gear.
Constructions where the chain runs under or through the pivot point are not optimal. The "squat" is then overcompensated. This can cause a slipping rear wheel when accelerating hard from a standstill. This is also accompanied by extra pedal kickback. In addition, extra pogo is created on a sprung front wheel.
It is impossible to simulate pogo-effects at a static role bank, because in that situation the forward driving force Fd does not push through the swing arm and frame to the center point of gravity!!
Often it is suggested a rider should learn by practice to apply his power smoothly, which would avoid pogo. This is impossible, see e.g. measurements below from The Pedaling Technique of Elite Endurance Cyclists:

According to the figure a cyclist delivers by far the most power while stretching the leg. Therefore this stretching phase is majorly responsible for the delivered power. At the top and bottom dead center minor forces are delivered by leg muscles. This makes considerable pogo-effects unevitably. Pogo-free pedaling is therefore only possible if less force is exerted when stretching the leg. However, this allows the leg muscles to deliver less pedaling power and that cannot be the intention.
Yet it is true, pogo-effects can be less, if one uses a high pedal-frequency (and lower pedaling force).
Some explanation about the same kind of problem with cars.
If cars accelerate very fast, the rear-side of a car with suspension will be pushed down and the front will move upwards (squat).
At the next figure it is shown how the rear suspension of a rear-wheel-driven car should be constructed to compensate squat.

At the first drawing of this picture, squat is totally compensated by "anti-squat". This happens if the point of intersection of the bars (instant center) is at the "diagonal". This is the same optimal diagonal, as should be used at recumbents to avoid pogo!!
A demo-simulation-program with similar results can be downloaded from here.
This a program from drag-race-world, where one even overcompensates squat, to get extra pressure on the rearwheel.
The program gives the opportunity to adjust the 4-link for a Chevrolet Camaro and computes the resulting anti-squat.
Although the physical construction is totally different, the applied principle is the same.
The lower bar has the same function as the swing arm and pushes forwards, the upper bar has the same function as the chain and has a pulling force, to keep the differential steady upright.
Clearly one can recognize the triangular-construction as is drawn at the fourth figure of the intuitiv approach.
Information can be found at https://www.datamc.org/data-acquisition/suspension-data-analysis/suspension-analysis-squat/. Picture below was copied from this site.
The graphical simulation by Walter Zorn is a Java program that can be started under Windows 10 and 11 with Microsoft Edge in Internet Explorer mode or can be started under Chrome, Chromium or Edge with the extension CheerpJ.
This appendix still contains some extreme bicycle models, that were used to detect differencies with the simulation of Walter Zorn.
A fictitious Kreuzotter Xtreme is constructed, with center of gravity and swing arm pivot at height zero and a rear cog with the same size as the rearwheel.
Because the center of gravity is positioned at the road, the mass inertia does not cause any torque at the rear axle.
The chainforce Fc is perpendicular to the road and its size is exactly equal to the size of the forward driving force Fd.
The vector-sum of both forces has the same direction as the swing arm and delivers no pogo-effect (no forces to be compensated by suspension).
Notice, that if the center of gravity is on the road and the swing arm runs downwards from the rear axle, at any angle of the swing arm the optimal position of the middle chainwheel is on the road.
A second fictitious machine is the Kreuzotter Square
Swing arm pivot and middle chainwheel are positioned at the ICR (rotation center of the frame).
Chainforce Fc and forwards driving force Fd are equal and both horizontal forwards directed. At the rear axle there is the sum of both forces (two times chain force Fc).
The swing arm pushes backwards with the same force. The angle of the swing arm (height:length = 1:2) causes a downwards force, which is half of horizontal force (one times force Fc). This force is exactly equal to the downwards force Fw caused by mass inertia.
At the pivot the swing arm pushes forward with force two times chainforce Fc and upwards with one times Fc.
The chain pulls horizontal with 1 times chainforce Fc.
um of both forces is one times chainforces forwards (the expected forward driving force) and one times chainforce upwards (caused by mass inertia).
The forward force is directed through the center point of gravity and gives no rotation to the frame, the upward force is directed through the front axle and also cannot cause rotation.