Figure 5.2)
Click to enlarge
The following two theories assert special points through which the chain line (or extended chain line) must pass, in order to make a suspension non-reactive to pedaling.
Traditionally this has been taken as true, regardless of mass distribution or any other considerations. However, as understanding of bicycle rear suspensions has evolved in the bike industry, some now take this to be true, given various conditions, for example conditions on mass distribution and pivot location.
We will consider only the more restrictive theories here, since if special point theories are false, even when mass and so forth is taken into consideration, then they will certainly be false more generally.
We begin this section with a general proof that all special point theories are false, even those accounting for mass. We will employ Path Analysis in this demonstration.
However, it will be instructive to state the special point theories below, with some further comments. The second theory has a well-known name attached to it, so we will put Path Analysis to the test against the second theory to see which is really right.
This theory states that locating a mono-pivot pivot along the chain force line will eliminate suspension activation under pedaling. Most mono-pivot producers, including Santa Cruz, Marin, and Ellsworth's Aeon division produce bikes based on this theory. Some take this to mean with acceleration (Ellsworth) and some without (Santa Cruz). A notable exception is the Titus Loco Moto.
We have already given a general proof that all special point theories are false. However, since PCL is such a common theory in the bicycle industry, we wish to spare no effort in exposing the problems. In addition, a number of people with whom the author has had regular contact are interested in certain specific issues. So in Appendix A) “PCL Problems; Some Further Calculations.”, we do some further specific calculations to dispel any lingering doubts as to the erroneous nature of this theory.
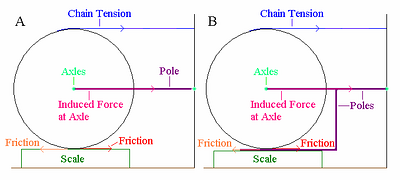
The one last issue worthy of mention here is an erroneous justification for PCL known as the “Locked Wheel Scenario”. It is reasoned that the large amount of friction between the rear wheel and the ground, under pedaling, is equivalent to a large amount of friction in the bearings, leading to a situation essentially equivalent to a locked wheel. This idea is false, since friction between the wheel and the ground does not directly involve the swingarm, as does friction in the bearings. To see this, consider Figure 5.2).

Figure 5.2)
Click to enlarge
Figure 5.2 A) shows our pole and wheel turned sideways, with the wheel resting on a scale. The scale will read the force between the wheel and the ground. Horizontal tension in the chain will not alter the scale reading. More to the point, friction exerted on the wheel (red), will also have no impact on scale reading, since it is directed horizontally. The same is true for friction acting on the scale (orange). There could be locking friction or no friction, and the scale reading would be the same because there are no vertical components of force involved.
Figure 5.2 B) again shows a pole and wheel, but this time friction is created in the wheel via a horizontal pole rubbing against the wheel. The horizontal pole is attached to a vertical pole, which in turn is attached to the swingarm pole. Friction acting on the horizontal pole (orange), pulls the pole forward, creating a torque on the vertical pole about the point where it meets the swingarm. This ultimately creates a torque on the swingarm pole about the green swingarm/wall axle. The vertical components of force occur where the vertical pole meets the swingarm pole. In this way, friction applied to the wheel feeds directly back into the swingarm, just as it would in the case of friction in the bearings. Horizontal chain tension will obviously lift the wheel, altering the reading on the scale.
Thus is dispelled the “Locked Wheel Scenario”.